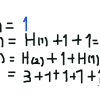【数学】 ハノイの塔について

プログラマの数学を読んでいる

プログラマの数学を読んでいる。ハノイの塔の漸化式がわからなかったので、自分なりの解釈で解いてみた。

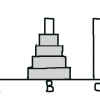
ハノイの塔

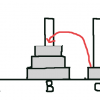
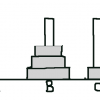
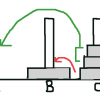
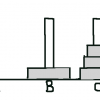
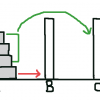
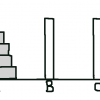
3本の柱がある。そこに円盤があり、その円盤は上に自分より小さいのを、下に自分より大きいのを置ける。

移動は一番上にある円盤を1枚ずつ移動できる。

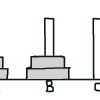
1枚ずつ移動した時、真ん中の柱Bへ移動する。

法則がある

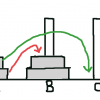
移動したあとで気がついたんだけど、円盤の塔に法則を見つけた。

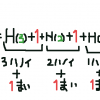
H(n) = H(n - 1) + 1 + H(n - 2) + 1 ... H(1) + 1 + 1

H(n - 1) + 1の部分はH(n - 1)がBではない柱へ移動させ、+ 1の部分が柱Bへ移動させる一番下の円盤。これをH(n - 1)の部分を1ずつ小さくしながらn - 1回繰り返していく。

一番最後の+ 1は一番小さな円盤を1回だけ動かすため必要。

これでn個の円盤を1から数えて法則に当てはめていけば最小移動回数が求められる。

プログラムで

Rubyで書いてみた。

#!ruby -Ks

def hanoi(i)
  if i == 0
    return 0
  elsif i > 0
    k = 0
    (i - 1).downto(1) {|j| k += hanoi(j) + 1 }
    return k + 1
  end
end

p hanoi(1)
p hanoi(2)
p hanoi(3)
p hanoi(4)
p hanoi(5)
p hanoi(6)

2012/11/02 13:48