【アルゴリズム】 シェルピンスキーの三角形

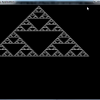
シェルピンスキーの三角形

パスカルの三角形の数字が奇数のときのみ、小さな三角形を描く。すると、再帰的な図形が出来上がる。

コード

C言語による最新アルゴリズム事典のP.422を参考に、DXRubyで記述。

#!ruby -Ks

require "dxruby"

SIZE = 12
N = 9

$triangle = Image.new((SIZE * 2) * N, (SIZE * 2) * N)

def triangle(x, y, num, color=[255,255,255])
  x1 = (x * SIZE)
  y1 = (y * SIZE)
  x2 = ((x + 1) * SIZE)
  y2 = ((y + 1) * SIZE)
  x3 = ((x - 1) * SIZE)
  y3 = ((y + 1) * SIZE)

  $triangle.triangle(x1, y1, x2, y2, x3, y3, color)
end

a = Array.new(N * 2 + 1) { 0 }
a[N] = 1
b = Array.new(N * 2 + 1) { 0 }

1.upto(N - 1) do |j|
  (N - j).upto(N + j) do |i|
    triangle(i, j, a[i]) if a[i] % 2 == 1 
  end

  (N - j).upto(N + j) {|i| b[i] = a[i - 1] + a[i + 1] }
  (N - j).upto(N + j) {|i| a[i] = b[i] }
end

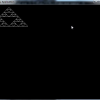
Window.loop do
  Window.draw(0, 0, $triangle)

  break if Input.keyPush?(K_ESCAPE)
end

考え方

とりあえず、小さく考えてみる。Nは9あたりがいいだろうか。

Nを設定すると、その倍+1の配列aが用意される。その配列には、真ん中になるN番目の要素に1を入れる。

縦jのループ

25、26行目の間にaをpで表示すると、結構理解しやすい。

横iのループ

ここが起点になっていて、配列aのi番目の要素が奇数だと、小さな三角形を描く。その時のループは必要最小限のループになっている。別に0からN*2+1番目まですべて調べても動作には問題はないと思う。無駄ってだけで。

三角形を描き終わった後

三角形を描き終わると、次のj列への準備を行う。配列bには、i番目の要素にa[i - 1]とa[i + 1]を足し算をした内容を入れる。aにそれを入れなおして次の列へ。足し算した中身は、Nが65になると結構大きい値になってしまう。ここを0と1にすることもできる。

DXRubyとwindow.cの違い

window.cというファイルをコンパイルしてこの図形を表示させているのが本書なんだけど、これをDXRubyで再現するには、上下反対にしなくてはならないらしい。少なくとも、そう思ったので、上下反対にしたコードになっている。

あと、Imageに突っ込んで使い回しが効くようにした。これでDXRubyで使い勝手が良くなったと言えるかな？もしかすると、Spriteクラスを使ったほうがいいかもしれないけど…

考えの助けになった本

プログラマの数学。数を減らして単純化したり、シェルピンスキーの三角形についての記述もあったので、理解の助けになった。

2012/11/30 18:58